Skip to main content

5.7.1 Marginal effects

The mfx() option is used to specify that marginal effects are to be estimated in addition to the usual logistic coefficients. This is preferred by many since marginal effects are easier to interpret than standard estimates.

It is possible to choose between four different types of marginal effects:

  • dydx: marginal effect = d(y)d(x)\dfrac{d(y)}{d(x)}

  • eyex: elasticity value = d(ln⁡y)d(ln⁡x)\dfrac{d(\ln y)}{d(\ln x)}

  • dyex: semi-elasticity = d(y)d(ln⁡x)\dfrac{d(y)}{d(\ln x)}

  • eydx: semi-elasticity = d(ln⁡y)d(x)\dfrac{d(\ln y)}{d(x)}


By combining the two options mfx() and mfx_at(), you can override the default measure. The following variants are available:

  • mfx_at(overall) (mean of the marginal effects measured over all x values) (default measure if this option is not used)

  • mfx_at(mean) (marginal effect measured at mean value of x)

  • mfx_at(median) (marginal effect measured at median value of x)

  • mfx_at(zero) (marginal effect measured at 0-value of x)


The mfx_at() option is usually used in combination with mfx(), for example:

 logit high_income male married age high_wealth, mfx(dydx) mfx_at(mean)


However, you may also just use mfx_at(). Thus, the standard variant mfx(dydx) is used.

The following alternative regression expressions will present the same marginal effect values:

 logit high_income male married age high_wealth, mfx(dydx) mfx_at(overall)

 logit high_income male married age high_wealth, mfx_at(overall)

 logit high_income male married age high_wealth, mfx(dydx)


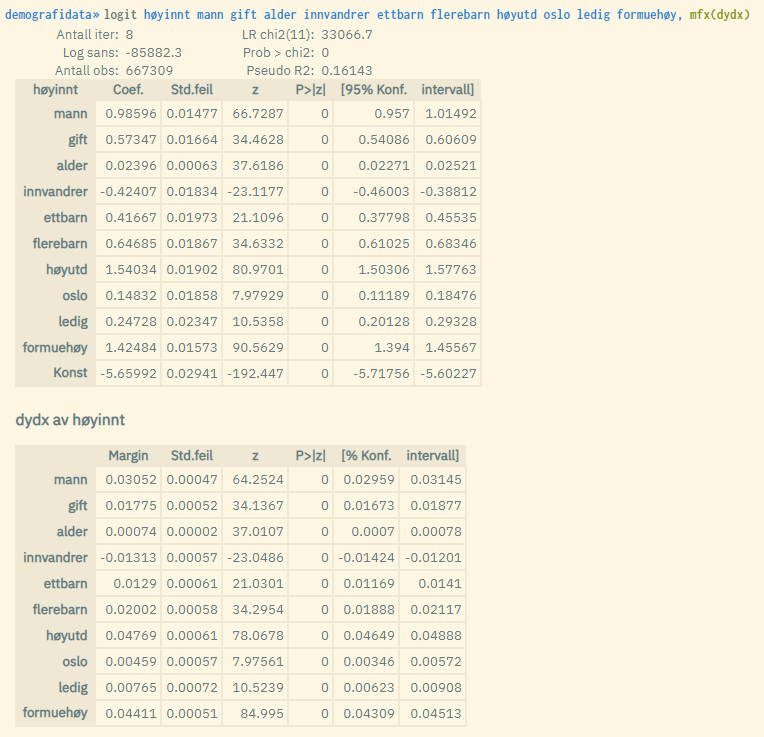
Example of a logit regression including estimated average marginal effects (most commonly used). Common logistical estimates are listed first, then the marginal effects: